Berikut ini adalah video tentang bagaimana membuat aplikasi Cleint Server dengan bahasa pemrograman C#. Teknik ini bisa digunakan untuk membuat
hal-hal semisal aplikasi chat (bahkan yang berbasis mobile Android dan Iphone). Juga bisa digunakan untuk membuat aplikasi Gojek/Grab-Bike/Uber dan aplikasi aplikasi transprotasi online sejenis.
Adapun source code untuk projectnya bisa didownload di link berikut ini:
https://github.com/gunungloli666/simple--wpf-client-server-chat
Sesungguhnya shalat itu mencegah dari (perbuatan-perbuatan) keji dan mungkar
Q.S. Al-'Ankabut Ayat 45
Friday, July 7, 2017
Thursday, April 13, 2017
Saturday, December 24, 2016
Teorema Fundamental Dalam Aritmatika
Teorema fundamental dalam aritmatika merupakan teorema paling dasar dalam aritmatika, dalam artian semua teorema-teorema lain diturunkan dari teorema ini (kira-kira seperti itu).
Ada dua pernyataan yang perlu diklarifikasi dalam Teorema Fundamental Aritmatika ini, pertama eksistensi, dan kedua keunikannya. Pernyataan lengkapnya adalah setiap bilangan bulat lebih dari $1$ adalah bilangan prima atau produk dari bilangan prima dan produk ini unik dalam artian untuk sebuah bilangan, maka hanya ada satu cara memfaktorkannya ke dalam bilangan prima.
Misalnya, 1200 hanya bisa dinyatakan ke dalam perkalian $1200 = 3 \times 2 \times 2 \times 2 \times 2 \times 5 \times 5 $.
Ada dua pernyataan yang perlu diklarifikasi dalam Teorema Fundamental Aritmatika ini, pertama eksistensi, dan kedua keunikannya. Pernyataan lengkapnya adalah setiap bilangan bulat lebih dari $1$ adalah bilangan prima atau produk dari bilangan prima dan produk ini unik dalam artian untuk sebuah bilangan, maka hanya ada satu cara memfaktorkannya ke dalam bilangan prima.
Misalnya, 1200 hanya bisa dinyatakan ke dalam perkalian $1200 = 3 \times 2 \times 2 \times 2 \times 2 \times 5 \times 5 $.
Wednesday, December 21, 2016
Membuktikan bahwa ada Tak Terhingga Bilangan Prima dalam bentuk 4 n + 3
Teorema. Ada tak berhingga banyaknya bilangan prima dalam bentuk $4 n + 3$.
Sebenarnya ini merupakan teorema perluasan dari teorema Euclid bahwa ada tak berhingga jumlah bilangan prima.
Untuk membuktikan teorema ini, terdapat sebuah lemma yang harus diketahui, yakni
Lemma. Jika $a$ dan $b$ adalah dua buah bilangan bulat dalam bentuk $4n + 1$ maka produk atau hasil perkaliannya juga dalam bentuk $4 n + 1$.
Pertama kita harus ingat kembali ( maaf, postingan tentang ini nanti dibuat kemudian) bahwa setiap bilangan bulat itu berada pada dua keadaan yakni bilangan prima atau hasil perkalian dari bilangan prima (biasa disebut bilangan komposit). Misalnya $3$ itu bilangan prima, $4$ itu bilangan komposit $ 4 = 2 \cdot 2 $, $5$ itu bilangan prima, $6 = 2 \cdot 3$ bilangan komposit, $7$ bilangan prima, $8 = 2 \cdot 2 \cdot 2$ bilangan prima, $9 = 3 \cdot 3$, $10 = 2 \cdot 5$ bilangan komposit, $11$ bilangan prima, dst... dst...
Sebenarnya ini merupakan teorema perluasan dari teorema Euclid bahwa ada tak berhingga jumlah bilangan prima.
Untuk membuktikan teorema ini, terdapat sebuah lemma yang harus diketahui, yakni
Lemma. Jika $a$ dan $b$ adalah dua buah bilangan bulat dalam bentuk $4n + 1$ maka produk atau hasil perkaliannya juga dalam bentuk $4 n + 1$.
Pertama kita harus ingat kembali ( maaf, postingan tentang ini nanti dibuat kemudian) bahwa setiap bilangan bulat itu berada pada dua keadaan yakni bilangan prima atau hasil perkalian dari bilangan prima (biasa disebut bilangan komposit). Misalnya $3$ itu bilangan prima, $4$ itu bilangan komposit $ 4 = 2 \cdot 2 $, $5$ itu bilangan prima, $6 = 2 \cdot 3$ bilangan komposit, $7$ bilangan prima, $8 = 2 \cdot 2 \cdot 2$ bilangan prima, $9 = 3 \cdot 3$, $10 = 2 \cdot 5$ bilangan komposit, $11$ bilangan prima, dst... dst...
Monday, December 19, 2016
Membuktikan Bahwa Bilangan e Irasional Versi Fourier
Dalam tutorial ini, saya akan memberikan penjelasan tentang pembuktian irasionalitas bilangan $e$. Ada banyak sebenarnya pembuktian irasionalitas bilangan $e$ ini, namun yang paling cantik dan paling populer itu adalah pembuktian dari Joseph Fourier ini.
Seperti kebanyakan pembuktian tentang irasionalitas lainnya, pemubuktian irasionalitas $e$ ini menggunakan metode pembuktian dengan kontradiksi. Jadi jika $e$ adalah bilangan rasional, maka tentu dapat dinyatakan sebagai perbandingan dua buah bilangan bulat positif $a$ dan $b$ yakni $e = \frac{a}{b} $. Selanjutnya Fourier mendefinisikan sebuah definisi yang cukup cantik yakni \begin{eqnarray} x = b ! \left( e - \sum_{n = 0 }^{b} \frac{1}{n !} \right) \nonumber \end{eqnarray} Tentu pembaca ada yang bertanya-tanya, dari mana Fourier mendapatkan defenisi seperti ini, kok tiba-tiba saja ada pola yang begitu menarik di awal pembuktian ini?
Seperti kebanyakan pembuktian tentang irasionalitas lainnya, pemubuktian irasionalitas $e$ ini menggunakan metode pembuktian dengan kontradiksi. Jadi jika $e$ adalah bilangan rasional, maka tentu dapat dinyatakan sebagai perbandingan dua buah bilangan bulat positif $a$ dan $b$ yakni $e = \frac{a}{b} $. Selanjutnya Fourier mendefinisikan sebuah definisi yang cukup cantik yakni \begin{eqnarray} x = b ! \left( e - \sum_{n = 0 }^{b} \frac{1}{n !} \right) \nonumber \end{eqnarray} Tentu pembaca ada yang bertanya-tanya, dari mana Fourier mendapatkan defenisi seperti ini, kok tiba-tiba saja ada pola yang begitu menarik di awal pembuktian ini?
Membuktikan Bahwa Akar Dua Irasional Versi Euclid
Sebenarnya ini merupakan tutorial klasik yang diajarkan hampir di seluruh dunia, namun ternyata menurut salah satu pengarang buku Elektrodinamika yang bernama David J. Griffith ternyata menyimpan sebuah lelucon filosofis yang cukup halus (bisa dilihat di lampiran buku Introduction to Electrodynamics karya beliau).
Pembuktian yang biasa diajarkan di sekolah-sekolah kita itu seperti ini (pembuktian dengan kontradiksi):
1. Asumsikan bahwa $\sqrt{2}$ adalah bilangan rasional sehingga terdapat dua bilangan yang rasionya adalah $\sqrt{2}$.
Pembuktian yang biasa diajarkan di sekolah-sekolah kita itu seperti ini (pembuktian dengan kontradiksi):
1. Asumsikan bahwa $\sqrt{2}$ adalah bilangan rasional sehingga terdapat dua bilangan yang rasionya adalah $\sqrt{2}$.
Saturday, June 18, 2016
Menggunakan Java Standard Library dari Matlab
Dalam tulisan kali ini saya ingin memberikan sedikit pemahaman kepada pembaca mengenai bagaimana caranya menggunakan fitur-fitur yang tersedia pada bahasa Java standard oracle (Java Standard Library) untuk keperluan komputasi di MATLAB.
Sebenarnya tulisan ini hanya merupakan rangkuman tentang tulisan yang tertera di blog ini. Di mana dalam blog tersebut saya mendapatkan sebuah ilmu yang sangat bermanfaat yakni tentang bagaimana memanggil java standard library dari program MATLAB selama runtime.
Friday, May 20, 2016
Saturday, March 12, 2016
Membuat aplikasi GUI dengan GUIDE di MATLAB
Dalam tutorial kali ini saya ingin mempertontonkan kepada pembaca tentang bagaimana cara membuat aplikasi GUI sederhana di MATLAB. Mudah-mudahan ini bisa bermanfaat. Saya akan mendemokan kasusnya untuk hal yang sederhana, selanjutnya pembaca tinggal menyesuaikannya untuk kasus yang lebih rumit, ya… yang smart dikit lah bro….
1. Step pertama buka MATLAB, yang tampilan keseluruhan window-nya kira-kira seperti berikut:
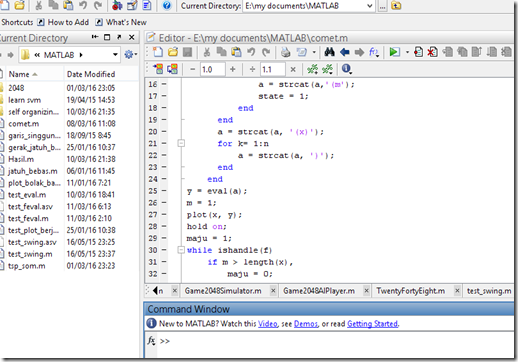
2. Jika sudah dibuka, selanjutnya di command window-nya ketikkan perintah guide dan tekan ENTER:

3. Pilih aja ‘BLANK Gui (default)’ dan klik ‘OK’ yang selanjutnya Anda akan digiring menuju tampilan sebagai berikut:
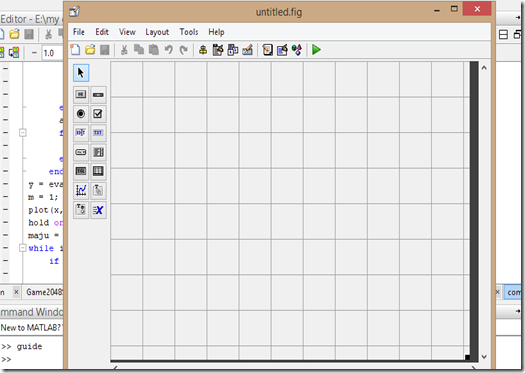
4. Jika sudah pencet CTRL + S atau pada menunya klik save as:

5. Dan save di komputer Anda dan beri nama misalnya test1:
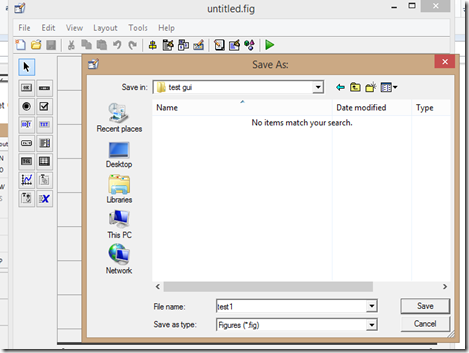
6. Jika sudah, nanti di folder itu akan terbuat (tergenerate) sebuah m file yang namanya itu menyesuaikan dengan nama .fig file yang sudah kita simpan tadi.
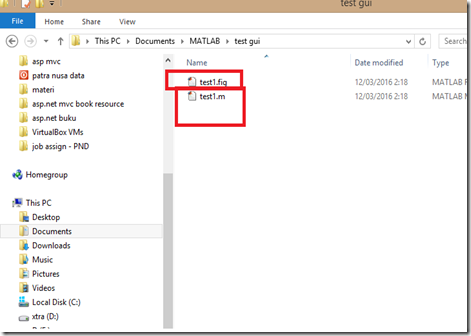
7. Dan ini secara otomatis akan tampil di editor MATLAB:
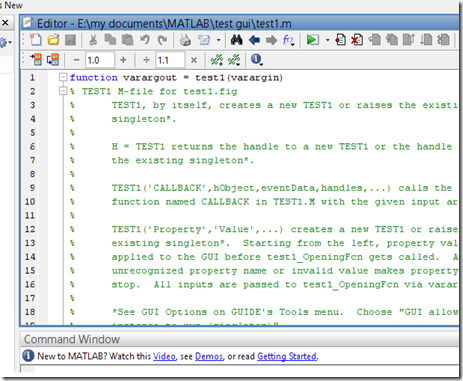
8. Hal yang perlu pembaca pahami adalah di file editor ini kita tidak boleh melakukan pengeditan secara sembarangan, karena nama-nama variabel atau function di file ini sudah disesuaikan dengan file .fig yang menjadi pasangannya. Di dalam m file ini terdapat opening-function yang dieksekusi ketika GUI nya pas mulai tampil. Dan ini fungsinya hampir miriplah dengan konstruktor di bahasa java. Untuk saya pribadi biasanya di opening-function ini saya taruh perintah clc, jadi ketika GUI nya tampil, maka command-windownya dibersihkan dulu.

9. Kita kemudian menambahkan beberapa control pada file fig nya tadi, misalnya sebuah button dan sebuah textfield (atau dalam terminologi MATLAB nya disebut sebagai static text), caranya tinggal di drag n drop aja dari panel sebelah kiri:

10. Selanjutnya untuk mengeset nilai dari control-control tadi, tinggal klik kanan kemudian ‘Property Inspector’ dan kemudian muncul window buat pengaturan properties-nya:
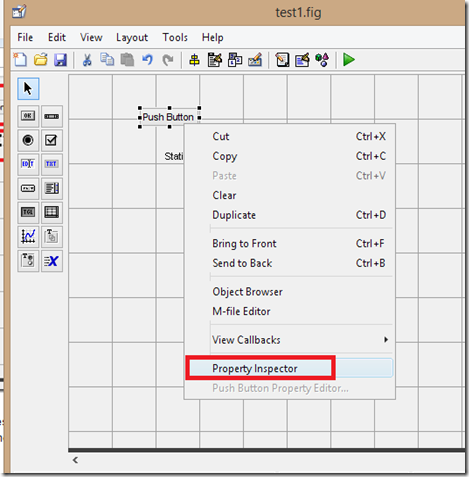
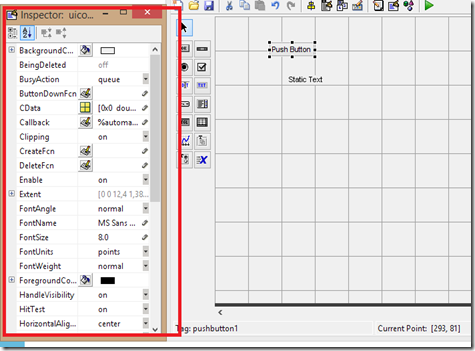
11. Di window property inspector itu selanjutnya kita bisa mengatur beberapa hal, misalnya dengan mengganti text dari button-nya menjadi sesuatu yang lain, contoh kita ganti textnya menjadi ‘BUTTON MAKAN’, caranya lihat ke baris String, dan pada kolom di kanannya berikan text sesuai dengan yang Anda kehendaki, setelah itu CTRL + S:

12. Jadi Button tadi sudah berubah tampilan

13. Untuk memberikan fungsi pada tombol tadi, misalnya jika dia di-klik akan menghasilkan nilai tertentu, maka hal yang dilakukan adalah mengatur variabel pada property inspector nya yakni pada baris CallBack. Nah di situ kan di kolom sebelah kanan ada icon tertentu yang Anda boleh klik:

14. Jika sudah di-klik, nanti di m file nya ter-generate (maaf saya kurang tahu apa bahasa Indonesia yang tepat untuk menerjemahkan kata generate, tapi menurut Prof. Bobby Eka Gunara yang jadi dosen di ITB, itu diterjemahkan sebagai membangkitkan, tapi berhubung ini membahas MATLAB maka saya abaikan dulu ajaran beliau itu) sebuah fungsi yang disesuaikan dengan nama dari tombol tadi. Nama tombol ini bisa dilihat pada baris tag pada property inspector:

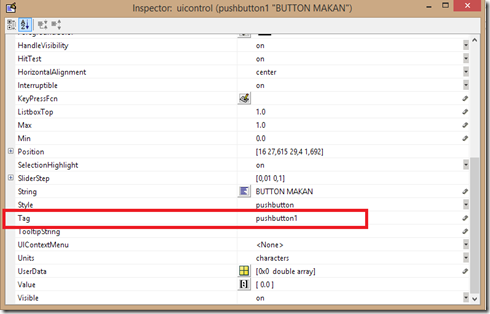
15. Jadi jika kita meng-klik tombol/button tadi, maka apapun perintah yang valid yang ditempatkan di dalam fungsi pushbutton1_Callback ini akan dieksekusi.
16. Selain itu, fungsi utama dari baris Tag dari property Inspector ini adalah agar kita bisa mengakses button tadi dari m-file. Misalnya kita ingin mengeprint text pada button tadi ketika button tersebut di klik, maka yang dilakukan adalah tempatkan perintah berikut pada function pushbutton1_Callback:

Jadi dapat kita lihat, bahwa handles di sini mengacu pada parameter ketiga dari function pushbutton1_Callback, yang mana ini menyimpan global variabel dari m file nya yang merupakan nilai-nilai yang diset pada fig file. Jadi dalam kasus pushbutton1, handles.pushbutton1 merupakan tag dari button ini. Itu yang kita panggil dan kita tampung dalam variabel y. Kemudian dengan get(y, ‘string’) maka kita mengambil nilai string nya atau text yang ditampilan pada pushbutton1. Dan ini akan ditampilkan pada output.
Sebenarnya banyak hal sih yang bisa kita atur dari property inspector ini.
1. Step pertama buka MATLAB, yang tampilan keseluruhan window-nya kira-kira seperti berikut:

2. Jika sudah dibuka, selanjutnya di command window-nya ketikkan perintah guide dan tekan ENTER:

3. Pilih aja ‘BLANK Gui (default)’ dan klik ‘OK’ yang selanjutnya Anda akan digiring menuju tampilan sebagai berikut:

4. Jika sudah pencet CTRL + S atau pada menunya klik save as:

5. Dan save di komputer Anda dan beri nama misalnya test1:

6. Jika sudah, nanti di folder itu akan terbuat (tergenerate) sebuah m file yang namanya itu menyesuaikan dengan nama .fig file yang sudah kita simpan tadi.

7. Dan ini secara otomatis akan tampil di editor MATLAB:

8. Hal yang perlu pembaca pahami adalah di file editor ini kita tidak boleh melakukan pengeditan secara sembarangan, karena nama-nama variabel atau function di file ini sudah disesuaikan dengan file .fig yang menjadi pasangannya. Di dalam m file ini terdapat opening-function yang dieksekusi ketika GUI nya pas mulai tampil. Dan ini fungsinya hampir miriplah dengan konstruktor di bahasa java. Untuk saya pribadi biasanya di opening-function ini saya taruh perintah clc, jadi ketika GUI nya tampil, maka command-windownya dibersihkan dulu.

9. Kita kemudian menambahkan beberapa control pada file fig nya tadi, misalnya sebuah button dan sebuah textfield (atau dalam terminologi MATLAB nya disebut sebagai static text), caranya tinggal di drag n drop aja dari panel sebelah kiri:

10. Selanjutnya untuk mengeset nilai dari control-control tadi, tinggal klik kanan kemudian ‘Property Inspector’ dan kemudian muncul window buat pengaturan properties-nya:


11. Di window property inspector itu selanjutnya kita bisa mengatur beberapa hal, misalnya dengan mengganti text dari button-nya menjadi sesuatu yang lain, contoh kita ganti textnya menjadi ‘BUTTON MAKAN’, caranya lihat ke baris String, dan pada kolom di kanannya berikan text sesuai dengan yang Anda kehendaki, setelah itu CTRL + S:

12. Jadi Button tadi sudah berubah tampilan

13. Untuk memberikan fungsi pada tombol tadi, misalnya jika dia di-klik akan menghasilkan nilai tertentu, maka hal yang dilakukan adalah mengatur variabel pada property inspector nya yakni pada baris CallBack. Nah di situ kan di kolom sebelah kanan ada icon tertentu yang Anda boleh klik:

14. Jika sudah di-klik, nanti di m file nya ter-generate (maaf saya kurang tahu apa bahasa Indonesia yang tepat untuk menerjemahkan kata generate, tapi menurut Prof. Bobby Eka Gunara yang jadi dosen di ITB, itu diterjemahkan sebagai membangkitkan, tapi berhubung ini membahas MATLAB maka saya abaikan dulu ajaran beliau itu) sebuah fungsi yang disesuaikan dengan nama dari tombol tadi. Nama tombol ini bisa dilihat pada baris tag pada property inspector:


15. Jadi jika kita meng-klik tombol/button tadi, maka apapun perintah yang valid yang ditempatkan di dalam fungsi pushbutton1_Callback ini akan dieksekusi.
16. Selain itu, fungsi utama dari baris Tag dari property Inspector ini adalah agar kita bisa mengakses button tadi dari m-file. Misalnya kita ingin mengeprint text pada button tadi ketika button tersebut di klik, maka yang dilakukan adalah tempatkan perintah berikut pada function pushbutton1_Callback:

Jadi dapat kita lihat, bahwa handles di sini mengacu pada parameter ketiga dari function pushbutton1_Callback, yang mana ini menyimpan global variabel dari m file nya yang merupakan nilai-nilai yang diset pada fig file. Jadi dalam kasus pushbutton1, handles.pushbutton1 merupakan tag dari button ini. Itu yang kita panggil dan kita tampung dalam variabel y. Kemudian dengan get(y, ‘string’) maka kita mengambil nilai string nya atau text yang ditampilan pada pushbutton1. Dan ini akan ditampilkan pada output.
Sebenarnya banyak hal sih yang bisa kita atur dari property inspector ini.
Subscribe to:
Comments (Atom)